一、 概述
强化学习算法可以分为三大类:value based, policy based 和 actor critic。常见的是以DQN为代表的value based算法,这种算法中只有一个值函数网络,没有policy网络,以及以DDPG,TRPO为代表的actor-critic算法,这种算法中既有值函数网络,又有policy网络。
说到DQN中有值函数网络,这里简单介绍一下强化学习中的一个概念,叫值函数近似。在基本概念这篇中有讲过,一个state action pair \((s, a)\)对应一个值函数\(Q(s, a)\)。理论上对于任意的\((s, a)\)我们都可以由公式求出它的值函数,即用一个查询表lookup table来表示值函数。但是当state或action的个数过多时,分别去求每一个值函数会很慢。因此我们用函数近似的方式去估计值函数: \[\hat{Q}(s, a, w) \approx Q_\pi(s, a)\]
这样,对于未出现的state action也可以估计值函数。
至于近似函数,DQN中用的是神经网络,当然如果环境比较简单的话用线性函数来近似也是可以的。
DQN算法原文链接: 2013版(arxiv) 2015版(nature)
二、算法原理
在基本概念中有说过,强化学习是一个反复迭代的过程,每一次迭代要解决两个问题:给定一个策略求值函数,和根据值函数来更新策略。
上面说过DQN使用神经网络来近似值函数,即神经网络的输入是state \(s\),输出是\(Q(s, a), \forall a \in \mathcal{A}\) (action space)。通过神经网络计算出值函数后,DQN使用\(\epsilon-greedy\)策略来输出action(第四部分中介绍)。值函数网络与\(\epsilon-greedy\)策略之间的联系是这样的:首先环境会给出一个obs,智能体根据值函数网络得到关于这个obs的所有\(Q(s, a)\),然后利用\(\epsilon-greedy\)选择action并做出决策,环境接收到此action后会给出一个奖励Rew及下一个obs。这是一个step。此时我们根据Rew去更新值函数网络的参数。接着进入下一个step。如此循环下去,直到我们训练出了一个好的值函数网络。
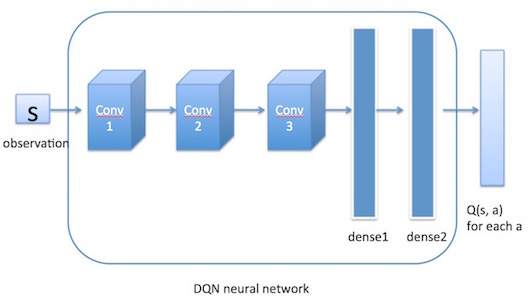
那么每次迭代如何更新神经网络的参数呢?
与机器学习类似,首先会定义一个loss function,然后使用梯度下降GD来更新参数。接下来首先介绍DQN的loss function,它与Q-Learning的非常类似,只是添加了一个target Q function。然后会介绍除此之外,DQN在Q-Learning上所做的改进。
1、Loss Function
\[L(\omega) = E[(R + \gamma \cdot max_{a'}Q(s', a'; \omega^-) - Q(s,a; \omega))^2]\] 这个公式表面上看起来很复杂,实际上很好理解,它就是一个残差模型,和我们平常见的最小二乘法很类似,真实值与预测值之间的差的平方。预测值就是\(Q(s,a; \omega)\),它是神经网络的输出。“真实值”略微有一点复杂。
想象一下假如我们想求出\((s, a)\)的真实值函数\(Q(s, a)\)。它表示我从state \(s\)开始出发,并采取action \(a\)的话,我所能得到的整体收益的期望值。一种可能的情况是,我们知道环境的模型。这在强化学习中也叫Model Based RL。即我们知道状态转移概率矩阵:当处于\((s, a)\)时,下一个到达的状态可能是什么,并且到达每一个状态的概率是什么;我们还知道奖励函数:当处于\((s, a)\)时,得到的立即回报的期望值是什么;另外还知道折扣因子。由此,我们便可以通过贝尔曼方程来求解值函数。这种情况下我们可能也并不需要神经网络近似值函数之类的,直接由策略迭代或值迭代便可以求出最优策略。具体方法可以看一下MDP。
另一种情况就是Model Free RL:不管有没有环境模型,反正我不用。那么在不知道环境模型的情况下如何求解值函数呢?答案就是采样。强化学习中有多种采样的方法,这里简单介绍一下:
(1) Monte Carlo

- MC使用一个完整的episode去更新值函数,因此它需要从\(S_t\)到Terminal state的完整样本。
- 而且需要等到episode结束才能更新值函数。
- 由于有一条完整的样本,它可以计算出return,而值函数是return的期望,所以我们可以用return去更新值函数。
(2) Temporal Difference / SarSa
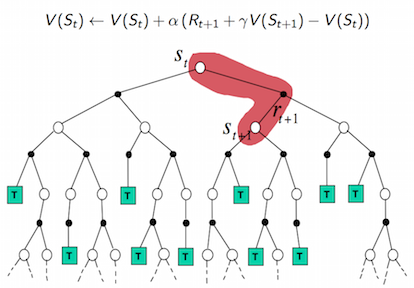
- 与MC不一样的是,TD不需要完整的样本,它只依赖下一个step的值函数,即它用\(V(S_{t+1})\) 去更新 \(V(S_t)\) (TD), 或用 \(Q(S_{t+1}, a_{t+1})\) 去更新 \(Q(S_t, a_t)\) (SarSa)
- 它不用等到episode结束,每走一步就可以更新值函数。
- 它不是用的真实的return值来更新值函数,而是用的一个估计值去更新另一个估计值的思想。
另外还有\(TD(\lambda)\) (或 \(SarSa(\lambda)\))方法,由于DQN中不涉及,暂不介绍。
DQN属于Model Free的强化学习算法,它需要采样。且同SarSa类似,只依赖下一个step的值函数。但它更新值函数的方式与SarSa又有所不同。下面介绍从SarSa到Q-Learning再到DQN的更新值函数的方式。
(1) SarSa
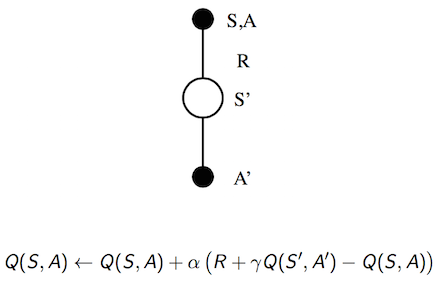
SarSa中更新值函数的公式为: \[Q(s, a) \leftarrow Q(s, a) + \alpha [R + \gamma Q(s', a') - Q(s, a)]\] 也称它的target是 \(R_{t+1} + \gamma Q(S_{t+1}, a_{t+1})\)。理解这个target代表的意义: \[ \begin{equation} \begin{split} V(s) &= E[G_t | S_t = s] \\ &= E[R_{t+1} + \gamma G_{t+1} | S_t=s] \\ &= E[R_{t+1} + \gamma V(S_{t+1}) | S_t=s] \end{split} \nonumber \end{equation} \] 将V换成Q的话我们可以看到,SarSa target \(R_{t+1}+ \gamma Q(S_{t+1}, a_{t+1})\) 是 \(Q(S_t, a_t)\) 的估计值。
在值函数近似中,我们都是使用target来替代真实的值函数,即Loss中的真实值。
前面说过DQN是使用\(\epsilon-greedy\)策略来输出action,SarSa和Q-Learning也是。SarSa中使用\(\epsilon-greedy\)策略生成action \(a_{t+1}\),随即又用 \(a_{t+1}\)处对应的值函数来计算target,更新上一步的值函数。这种学习方式又称为On-policy。
SarSa属于On-policy Learning,而Q-Learning属于Off-policy Learning。
(2) Q-Learning
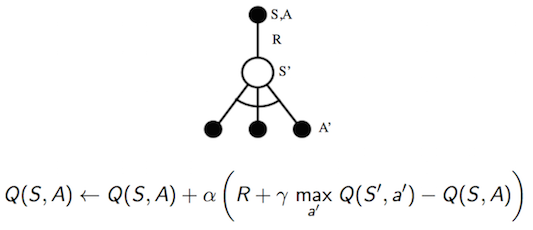
Q-Learning的target是 \(R_{t+1} + \gamma max_{a'} Q(S_{t+1}, a')\)。它使用 \(\epsilon-greedy\)策略来生成action \(a_{t+1}\),但用来计算target的action却不一定是\(a_{t+1}\),而是使得 \(Q(S_{t+1}, a)\)最大的action。这种产生行为的策略和进行评估的策略不一样的方法称为Off-policy方法。对于Q-Learning来说,产生行为的策略是\(\epsilon-greedy\),而进行评估的策略是greedy。
(3) DQN
Off-policy是Q-Learning的特点,DQN中也延用了这一特点。而不同的是,Q-Learning中用来计算target和预测值的Q是同一个Q,也就是说使用了相同的神经网络。这样带来的一个问题就是,每次更新神经网络的时候,target也都会更新,这样会容易导致参数不收敛。回忆在有监督学习中,标签label都是固定的,不会随着参数的更新而改变。
因此DQN在原来的Q网络的基础上又引入了一个target Q网络,即用来计算target的网络。它和Q网络结构一样,初始的权重也一样,只是Q网络每次迭代都会更新,而target Q网络是每隔一段时间才会更新。DQN的target是 \(R_{t+1} + \gamma max_{a'} Q(S_{t+1}, a'; \omega^{-})\)。用 \(\omega^{-}\)表示它比Q网络的权重 \(\omega\)更新得要慢一些。
理解了DQN的target之后也就可以理解DQN的Loss Function了。
2、DQN所做的改进
相比于Q-Learning,DQN做的改进:一个是使用了卷积神经网络来逼近行为值函数,一个是使用了target Q network来更新target,还有一个是使用了经验回放Experience replay。
由于在强化学习中,我们得到的观测数据是有序的,step by step的,用这样的数据去更新神经网络的参数会有问题。回忆在有监督学习中,数据之间都是独立的。因此DQN中使用经验回放,即用一个Memory来存储经历过的数据,每次更新参数的时候从Memory中抽取一部分的数据来用于更新,以此来打破数据间的关联。
三、算法整体流程
- 首先初始化Memory D,它的容量为N;
- 初始化Q网络,随机生成权重\(\omega\);
- 初始化target Q网络,权重为\(\omega^- = \omega\);
- 循环遍历episode =1, 2, …, M:
- 初始化initial state \(S_1\);
- 循环遍历step =1,2,…, T:
- 用\(\epsilon-greedy\)策略生成action \(a_t\):以\(\epsilon\)概率选择一个随机的action,或选择\(a_t = max_a Q(S_t, a; \omega)\);
- 执行action \(a_t\),接收reward \(r_t\)及新的state \(S_{t+1}\);
- 将transition样本 \((S_t, a_t, r_t, S_{t+1})\)存入D中;
- 从D中随机抽取一个minibatch的transitions \((S_j, a_j, r_j, S_{j+1})\);
- 令\(y_j = r_j\),如果 \(j+1\)步是terminal的话,否则,令 \(y_j = r_j + \gamma max_{a'} Q(S_{t+1}, a'; \omega^-)\);
- 对\((y_j - Q(S_t, a_j; \omega))^2\)关于\(\omega\)使用梯度下降法进行更新;
- 每隔C steps更新target Q网络,\(\omega^- = \omega\)。
- 用\(\epsilon-greedy\)策略生成action \(a_t\):以\(\epsilon\)概率选择一个随机的action,或选择\(a_t = max_a Q(S_t, a; \omega)\);
- End For;
- End For.
附上原文的算法流程:

四、\(\epsilon-greedy\)策略
\(greedy\)策略,顾名思义,是一种贪婪策略,它每次都选择使得值函数最大的action,即\(a_t = max_a Q(S_t, a; \omega)\)。但是这种方式有问题,就是对于采样中没有出现过的(state, action) 对,由于没有评估,没有Q值,之后也不会再被采到。
其实这里涉及到了强化学习中一个非常重要的概念,叫Exploration & Exploitation,探索与利用。前者强调发掘环境中的更多信息,并不局限在已知的信息中;后者强调从已知的信息中最大化奖励。而\(greedy\)策略只注重了后者,没有涉及前者。所以它并不是一个好的策略。
而\(\epsilon-greedy\)策略兼具了探索与利用,它以\(\epsilon\)的概率从所有的action中随机抽取一个,以\(1- \epsilon\)的概率抽取\(a_t = max_a Q(S_t, a; \omega)\)。
强化学习正是因为有了探索Exploration,才会常常有一些出人意表的现象,才会更加与其他机器学习不同。例如智能体在围棋游戏中走出一些人类经验之外的好棋局。
参考资料:
David Silver的课程:www0.cs.ucl.ac.uk/staff/D.Silver/web/Teaching.html
